Paradigm of Making Machine Learn; Supervised, Unsupervised, and Reinforcement
Here we explain the standard notion of machine learning, a lot of example you see in the internet mostly a practical scenario. In this notes, we tries to explicitly define why! [On progress]
Machine Learning Paradigm
AI vs ML: Broad Goals vs Learning from Data. Artificial Intelligence (AI) is the overarching field concerned with building agents that perceive their environment and take actions to maximize their chances of success (Russell & Norvig, AI: A Modern Approach). Under this definition, even a simple routing algorithm qualifies as AI if it senses and acts upon its environment. However, AI encompasses a wide spectrum, from symbolic logic systems to robotics. Within AI, Machine Learning (ML) focuses specifically on enabling machines to improve performance through experience. ML discards the need for explicitly defined rules—instead, it empowers models to learn patterns, make predictions, and refine their behavior through data-driven updates.
\(f: \mathcal X\to \mathcal Y\) The Essence of Learning: From Instructions to Adaptation. Traditional programming requires humans to explicitly write down every rule through code that could be represented as a function $f$, mapping inputs to outputs. In contrast, machine learning reverses this process: we provide a dataset consisting of inputs $\mathcal X$ and corresponding outputs $\mathcal Y$, and the learning algorithm infers the function $f$ from the data. This paradigm allows machines to generalize from examples, adapting to new inputs without manual intervention.
A widely accepted technical definition of machine learning, attributed to Tom Mitchell, captures this idea formally:
A computer program is said to learn from experience E with respect to some class of tasks T and performance measure P, if its performance at tasks in T, as measured by P, improves with experience E. — T. Mitchell, Machine Learning, McGraw Hill, 1997
This definition highlights the core principle: learning occurs when performance improves through experience.
Three Pillars of Machine Learning.. Understanding their interaction is crucial to mastering the field:
- Data. A model’s success depends heavily on the volume, variety, and validity of its training data. Noisy or biased data can lead to poor generalization, no matter how sophisticated the model. OpenAI mention that he best thing ever happen to them is having a single person knowing what the right data quality have to had at minimum. (OpenAI’s Deep Research Team on Why Reinforcement Learning is the Future for AI Agents, Youtube, 2025)
- Model (Hypothesis Space). A model is a mathematical function $f: \mathcal X \to \mathcal Y$ that maps inputs to outputs. It defines the space of possible solutions (hypotheses). Models can be:
- Parametric, like linear regression, with a fixed number of parameters and faster training.
- Non-parametric, like k-NN or decision trees, which adapt complexity to data
- Deep Learning Models, which are multilayered neural networks capable of learning hierarchical representations from raw input.
- Algorithms (Optimization and Learning). Algorithms provide the machinery to tune model parameters by minimizing a loss function, a numerical measure of prediction error. Common techniques include gradient descent, stochastic optimization, and backpropagation in neural networks. The choice of optimization algorithm often affects both convergence speed and model robustness.
Types of Machine Learning Algorithms. It’s important to note that the classical division into supervised, unsupervised, and reinforcement learning is not a collectively exhaustive categorization of how machines can learn. These categories are helpful, but they shouldn’t be treated as axiomatic. Still, the traditional trio can be better understood through an insightful analogy popularized by Michael Littman (with my little modification) in his talk on the Reward Hypothesis, reflecting three perspectives on how intelligence might be built:
-
“Give a man a fish and he’ll eat for a day”, Traditional Programming. This approach provides the solution directly without the ability to adapt. It corresponds to traditional programming or GOFAI (Good Old-Fashioned AI), where the agent executes pre-programmed rules without learning from experience. We need to be always there making it adapts everytime.
-
“Teach a man to fish and he’ll eat for a lifetime”, Supervised Learning. Here, the agent is taught on how to do it. Formally, given labeled examples i.e inputs (fishing rod and its bait) and desired outputs (big fish), the agent learns a general rule to apply in the future about how the inputs and outputs correlate (how to get big fish from fishing rod and a bait). This is the essence of Supervised Learning, where the goal is to generalize from training data to unseen instances.
-
“Give a man a taste of a fish, and he’ll figure out how to get fish, even if the details change”, Optimization (Reinforcement Learning). This reflects a more autonomous and adaptive form of learning, where the agent discovers strategies through trial and error, guided only by rewards. Once the agent know the good taste of a fish, he’ll try to find a way to experience that good experience again. This captures the spirit of reinforcement learning, where intelligence is framed as sequential decision-making under uncertainty which might involve a lot of trial and erros.
Supervised Learning
\[\mathcal D = \{(x_i, y_i)\}_{i=0}^n\]Supervised Learning: Learning from Labeled Pairs. Supervised learning is where the algorithm is trained on a dataset consisting of input-output pairs. The goal is to learn a function $f: \mathcal{X} \to \mathcal{Y}$ that maps input features $x \in \mathcal{X}$ to output labels $y \in \mathcal{Y}$. This setting is widely used in classification (where $y_i\in \mathbb N$ representing specific class i.e 0 for dogs and 1 for cats) and regression tasks (where $y_i\in\mathbb R$). In the language of statistics is pretty simple, it basically find conditional distribution $P(Y\mid X)$.
Goal. It is natural for every problem to defined the goal first before the solution candidate. The goal is
- Learn the unknown nature mapping $f: \mathcal X\to\mathcal Y$ that generalize to unseen data i.e $\mathcal D_{unseen}$ such that $\mathcal D_{unseen}\cap \mathcal D =\emptyset$. Why generalize to unseen data? Because if not, it means we have to gathering every possibility which is impossible, we only could sample a few and reason about the other (gathering every image of dogs in this universe is impossible).
Assumption in Supervised Learning. These are the assumption before doign any supervise learning technique, the reason for these assumption will explain in later paragraph thgoughout the components.
- Independent and Identically Distributed (IID) Data. $(x_i, y_i)\sim p_{xy}$
- Relation between Features $X$ and Target $Y$ Exists. If they are independent then finding $P(Y\mid X)$ is useless.
- Sufficiently Large, High Quality, and Representative Training Data. Otherwise we couldn’t achieve even medium degree of generalization.
Formally Defining Goal. We need to measure how good our estimate/model $f$ in order to know how close we are to the goal. Let’s consider multiclass classification problem where $f(x_i)_{y_j}$ represent output of our model, probability of having class $y_j$, so in probability notation $f(x_i)_j=P(y_j\mid x_i)$. One measure is through likelihood which derived from categorical distribution. \(\begin{align} \mathcal L &= P(Y\mid X) \\ \mathcal L &= P(y_1, y_2, \dots, y_n\mid x_1, x_2, \dots, x_n) \\ \mathcal L &= P(y_1\mid x_1, \dots, x_n) + P(y_2\mid y_1, x_1, x_2, \dots, x_n) + \dots \\ \mathcal L &= \prod_{i=0}^n P(y_i\mid x_i) \\ \mathcal L &= \prod_{i=0}^n f(x_i)_{y_i} \end{align}\) The intuition is that, we want to maximize model’s probability given that we know pair of $x_i, y_i$ is true coming straight from the nature, it’s value has to close to 1. From (3) to (4), we use the assumption that between data points, they are independent. Independent between $x_i$ is the only way for the chain in (3) to break, otherwise it is computationally intractable and exhaustive data gathering. The objective of maximizing $\mathcal L$ is called Maximum Likelihood Estimation (MLE) which is very common in ML.
\[\ell: \mathcal Y\times\mathcal Y \to \mathbb R\]Loss Function We generalize the notion of loss as a function of true value $y$ and predicted value $\hat y$ as $\ell$, likelohood is one example. When we apply log into likelihood, $\log \mathcal L$, we can see that it has the same form as $\ell$. Since $\log \mathcal L\propto\mathcal L$, optimizing $\log\mathcal L$ equivalent of optimizing $\mathcal L$ proving that $\ell$ is general form of $\mathcal L$.
\[\begin{align} R(f) &= \mathbb E_{p(x, y)} \ell(y, f(x)) \\ \hat R(f) &= \frac{1}{n} \sum_{i=0}^n \ell(f(x_i), y_i) \end{align}\]Generalization Risk and Empirical Risk. Back into the main goal, we need to define generalization error since this is the true objective we want. The generalization error denoted as $R$ would be the expected loss our model get under the distribution $p(x, y)$. This comes into second assumption, we assume that for every pair of x and y, they come from the same unknown distribution. Otherwise computing the generalization expectation would be complicated because we can’t write it into a single form, multiple expectation must be used and how important one after another is another complex, unnecessary, and does not really make sense at all. Since computing expectation under whole distribution of x and y is impossible, we estimate using the idea of unbiased sample mean approximation. Called it Empirical risk $\hat R$, that measure the average of $\ell$ among finite dataset $\mathcal D$. By the notorious theory in statistics, the law of large number, $\hat R$ will closely be $R$ with probability almost 1 as $\vert D\vert$ approach $\infty$. The difference between the expected risk on unseen data and on the seen training data is known as the generalization gap that again approximated by corresponding empirical risk.
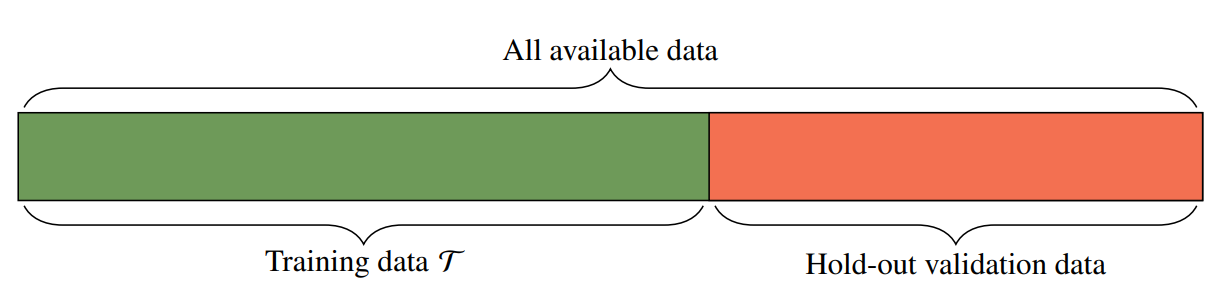
Measuring Generaliation Risk, Splitting the Data. Our real objective is engineering a model that has minimal generalization risk (expected risk) that is approximated by empirical risk. But we can’t directly create a model optimized from empirical risk directly, that way the approximation would be biased and would underestimate the true expected value. Formally, \(\begin{align} f &= \arg\min_{f'\in\mathcal F} \hat R(f') \\ f &= \arg\min_{f'\in\mathcal F} \frac{1}{\vert\mathcal D\vert} \sum_{x_i, y_i\in \mathcal D} \ell(y_i, f'(x_i)) \\ \mathbb E[\hat R(f)] &= \arg\min_{f'\in\mathcal F} \frac{1}{\vert\mathcal D\vert} \sum_{x_i, y_i\in \mathcal D} \ell(y_i, f'(x_i)) \le \hat R(f^\star),\quad \text{For all } f \in \mathcal F \end{align}\) (8) is the way we pick our model, one that minimize $\hat R$. (10) is a sign of bias estimation since whatever we do, we will always get the smaller empirical risk (with respect taken $\mathcal D$). This obviously almost impossible, if we gather additional data outside $\mathcal D$, there will always cases where our $\hat R(f)$ is not minimum among $f\in\mathcal F$. Hence usually we split our data into $\mathcal D = \mathcal D_{train}\cup\mathcal D_{val}\cup \mathcal D_{test}\quad$ $D_{train}$ is the training data for $f$, $\mathcal D_{val}$ is used to pick or hyperparameter tuning for deciding the best model, and $\mathcal D_{test}$ is the unbiased expected risk estimation (i.e the generalization capability, our true objective in SL). Note that any experiment continuation where decision is taken based on insight in $\mathcal D_{test}$ is prohibited, that way you would make $\mathcal D_{test}$ bias estimator which vanish the essence, recreating above event. The convention is writing $e_{train}, e_{val}, e_{test}$ as $\hat R$ calculated on each $\mathcal D_{train}, \mathcal D_{val}, \mathcal D_{test}$ respectively. This way we say that $e_{train}, e_{val}$ are bias estimation for empirical risk.
Various $\mathcal D$ Splitting Technique. In above splitting, $\mathcal D_{test}$ is kept fix which may not very representative. One example is Hold-out Validation Error or $e_{hold-out}$ which split into two train and test dataset. Test should be sampled randomly to avoid bias. Usually work for large representative data since the split ratio should make sure that both subset are representative to decrease variance.
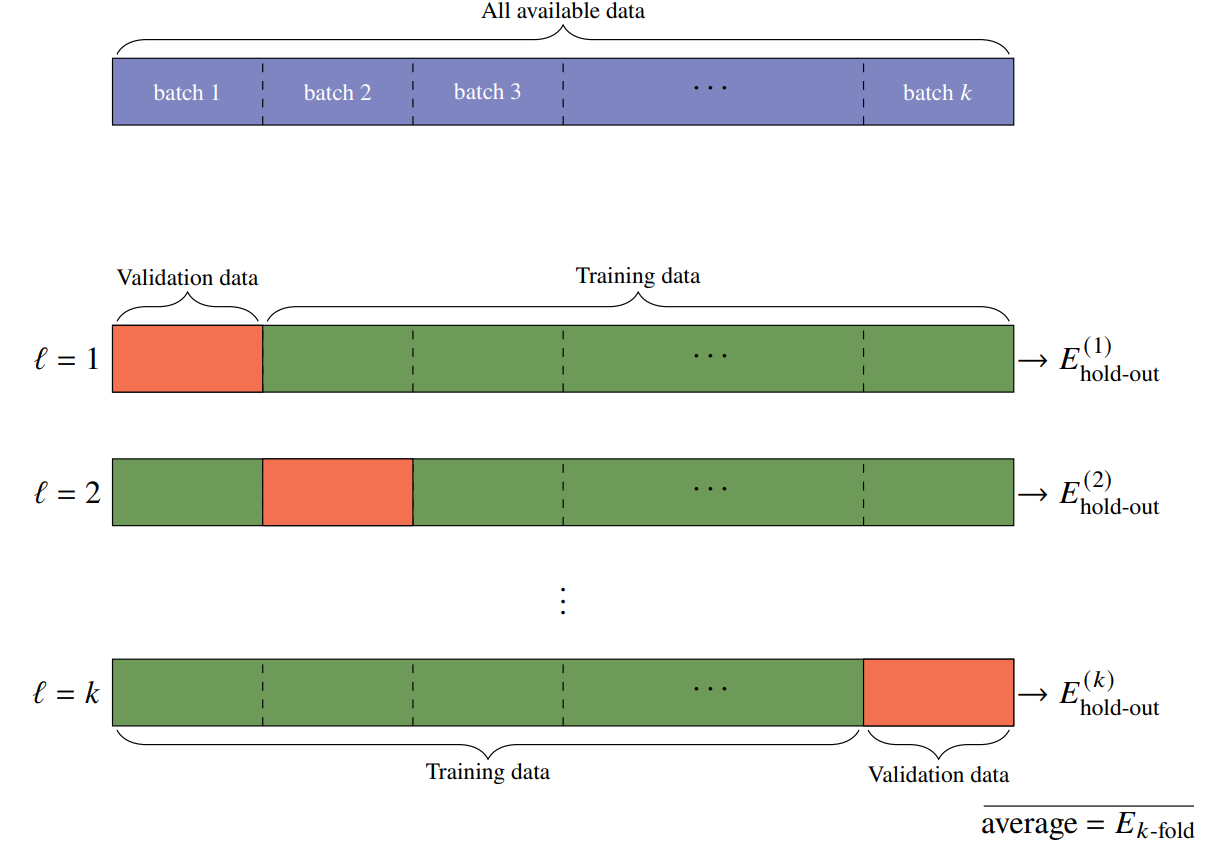
Another one is K-Fold to reduce variance in the error estimation where a model evaluated $K$ times along $K$ differerent training and test data, the average is the $e_{k-fold}$. Cross validation is more robust to high variance data (e.g small dataset) with the cost of $K$ times more expensive computation.
Parametric vs Non-Parametric Models, Capacity and Flexibility. Distinction between parametric and non-parametric models come from how we constrain the hypothesis (model) space. In parametric we assume a fixed form for the function $f$ with a limited number of parameters $\theta$. This assumption simplifies learning and computation but may restrict the model’s ability to capture complex patterns. In contrast, non-parametric models make fewer assumptions about the form of $f$ and allow complexity to grow with data. They can represent a wider range of functions and are more flexible but may require more data to generalize well. Examples include decision trees, k-nearest neighbors, and kernel methods. Parametric models are widely favored in practice because they are computationally efficient, scalable to large datasets, and easier to interpret and deploy.
Parametric Models and Learning via Gradient Descent. Let’s explore parametric differentiable models defined by a fixed set of parameters $\theta$ with every component of $f$ are differentiable. The model predicts $f(x; \theta)$, and the learning process involves finding the optimal $\theta$ that minimizes the empirical loss. The training becomes an optimization problem: \(\begin{align} \theta &= \arg\min_\theta \hat R \\ \theta &= \arg\min_\theta \frac{1}{\vert D\vert} \sum_{i=1}^n \ell(y_i, f(x_i;\theta)) \end{align}\) To solve this, we often use gradient descent, an iterative method that updates $\theta$ in the direction of the negative gradient of the loss: \(\theta \leftarrow \theta - \alpha\nabla_\theta\hat R(f(x_i;\theta), y_i)\) Where $\alpha$ is the set learning rate.
Linear Regression Model Example. Linear Regression is simple parametric differentiable model in the form of \(\begin{align} f(x;\theta) &= \theta_0 + \theta_1 x_1 + \theta_2 x_2 + \dots + \theta_p x_p \\ f(x;\theta) &= \vec \theta^T\vec x \end{align}\) Lets use Mean Squared Error loss function \(\begin{align} \ell(y, \hat y) &= (y-\hat y)^2 = (y-\theta^Tx)^2 \\ \hat R(y, \hat y) &= \frac{1}{\vert D\vert} \sum_i (y_i-\theta^Tx_i)^2 \end{align}\) Then the iterative parameter update would be \(\begin{align} \nabla_\theta\hat R &= \frac{2}{\vert D\vert}\sum_i(y_i-\theta^Tx_i)(-x_i) = \frac{2}{\vert D\vert}\sum_i(\theta^Tx_i-y_i)x_i \\ \theta&\leftarrow\theta - \alpha\frac{2}{\vert D\vert}\sum_i(\theta^Tx_i-y_i)x_i \end{align}\)
Non-Differentiable Loss Functions and Optimization Challenges. While many popular loss functions in supervised learning—such as mean squared error or cross-entropy—are differentiable and thus amenable to gradient-based optimization, some loss functions are non-differentiable, posing additional challenges. A common example is the 0-1 loss used in classification, defined as:
\[\ell(y, f(x)) = \begin{cases} 0\quad \text{if }f(x) = y \\ 1\quad \text{otherwise} \end{cases}\]This loss directly reflects classification accuracy but is not differentiable. To overcome this, we typically use surrogate losses that are smooth and differentiable, such as cross-entropy loss.
\[\ell(y_i, f(x_i)) = -\sum_{k=1}^K y_{i, k}\log f(x_i)_k\]In general, when working with non-differentiable objectives, we resort to subgradient methods, combinatorial optimization, or surrogate approximations, depending on the problem structure and computational constraints.
#TODO Unsupervised #TODO RL